Updating SI Base Units

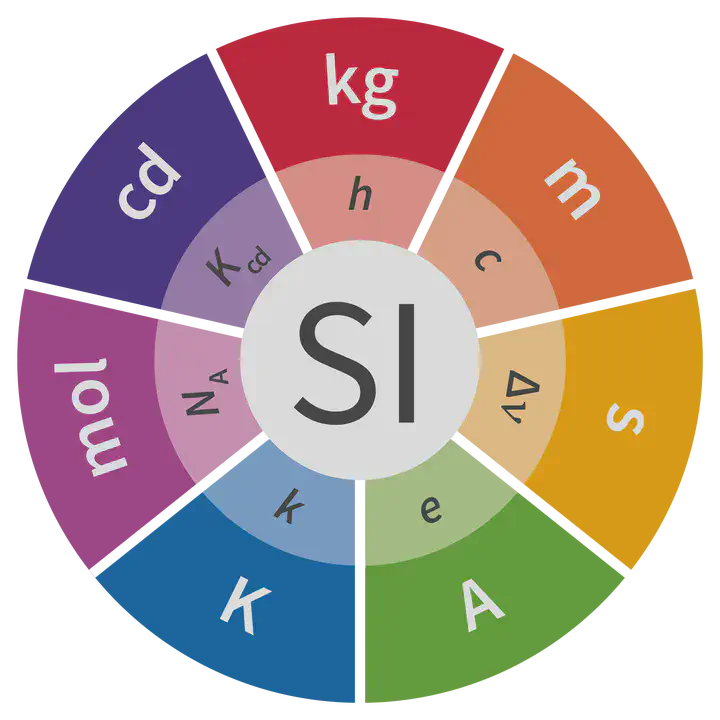
The International System of Units (SI) underwent a revision in 2018, with the redefinition of four of its seven base units, namely the kilogram (kg), the ampere (A), the kelvin (K) and the mole (mol).

This update was made to define all the units as a function of universal physical constants, something that had already been achieved previously for the second (1967) and the metre (1983). The following table summarises the relationship between each unit and the universal constant on which it is based:

Unit (symbol)	Universal constant (symbol)
Second (s)	Transition frequency of the caesium 133 atom ($\Delta\nu_\mathrm{Cs}$)
Metre (m)	Speed of light in vacuum ($c$)
Kilogram (kg)	Planck constant ($h$)
Ampere (A)	Elementary charge ($e$)
Kelvin (K)	Boltzmann constant ($k$)
Mole (mol)	Avogadro constant ($N_\mathrm A$)
Candela (cd)	Luminous efficacy of radiation of frequency $540\times 10^{12}\thinspace\mathrm{Hz}$ ($K_\mathrm{cd}$)

Current Definitions of SI Base Units

Second (s)

$$ 1\thinspace \mathrm s = \frac{9192631770}{\Delta\nu_\mathrm{Cs}}, $$

where $\Delta\nu_\mathrm{Cs} = 9192631770\thinspace\mathrm{Hz}$ is the unperturbed ground state hyperfine transition frequency of the caesium 133 atom.

Metre (m)

$$ 1\thinspace\mathrm m = \frac{9192631770}{299792458}\frac{c}{\Delta\nu_\mathrm{Cs}}, $$

where $c = 299792458\thinspace\mathrm{m\cdot s^{-1}}$ is the speed of light in vacuum.

Kilogram (kg)

$$ 1\thinspace\mathrm{kg} = \frac{(299792458)^2}{(6.62607015\times 10^{-34})(9192631770)}\frac{h\Delta\nu_\mathrm{Cs}}{c^2}, $$

where $h = 6.62607015\times 10^{-34}\thinspace\mathrm{kg\cdot m^2\cdot s^{-1}}$ is the Planck constant.

Ampere (A)

$$ 1\thinspace\mathrm{A} = \left(\frac{e}{1.602176634\times 10^{-19}}\right)\thinspace\mathrm{s^{-1}}, $$

where $e = 1.602176634\times 10^{-19}\thinspace\mathrm{A\cdot s}$ is the elementary charge.

Kelvin (K)

$$ 1\thinspace\mathrm{K} = \frac{1.380649\times 10^{-23}}{(6.62607015\times 10^{-34})(9192631770)}\frac{h\Delta\nu_\mathrm{Cs}}{k}, $$

where $k = 1.380649\times 10^{-23}\thinspace\mathrm{kg\cdot m^2\cdot s^{-2}\cdot K^{-1}}$ is the Boltzmann constant.

Mole (mol)

$$ 1\thinspace\mathrm{mol} = \frac{6.02214076\times 10^{23}}{N_\mathrm A}, $$

where $N_\mathrm A = 6.02214076\times 10^{23}\thinspace\mathrm{mol^{-1}}$ is the Avogadro constant.

Candela (cd)

$$ 1\thinspace\mathrm{cd} = \frac{1}{(6.62607015\times 10^{-34})(9192631770)^2 683}h(\Delta\nu_\mathrm{Cs})^2 K_\mathrm{cd}, $$

where $K_\mathrm{cd} = 683\thinspace\mathrm{cd\cdot sr\cdot kg^{-1}\cdot m^{-2}\cdot s^3}$ is the luminous efficacy of monochromatic radiation of frequency $540\times 10^{12}\thinspace\mathrm{Hz}$.